随着国民经济的不断发展，对电力的需求量越来越大，电力变压器随之向高电压、大容量方向发展。特别是目前三峡工程的建设，迫切需要生产出高电压、大容量的变压器。目前，国外已经制成1000MVA以上的巨型变压器，最大试制品为1800MVA，我国制造的变压器单台最大容量也已达到720MVA。

随着变压器单台容量的增大，低压绕组电流也随之增大，有的高达几万安培。由于大容量变压器低压绕组大多采用螺旋式结构，这样在低压绕组中势必存在一轴向电流分量，该分量随低压绕组电流的增大而增大。以往在计算变压器漏磁及损耗时，由于电流没有达到一定程度，再加上计算的复杂性、困难性，因此忽略了轴向电流分量对漏磁场的影响，认为绕组的线匝都是同轴圆环回路。而实际上变压器绕组都是用导线一匝紧挨一匝绕制而成的，每匝均具有螺旋性。特别是螺旋式绕组，随容量的增大，其螺旋性越来越明显。因此，一些变压器专家对是否应该忽略其螺旋性的影响，提出了疑问。特别是对于特大容量、大电流变压器，忽略了该分量的影响，能否会使变压器铁心及结构件产生局部过热。为了搞清这些问题，有必要对这一分量电流产生的漏磁场进行详细分析，并利用现代的电磁场计算技术，精确地计算出考虑这一电流分量后变压器漏磁场的分布，以及由此产生的损耗，这有助于在开发新产品时，采取措施，控制其产生的负效应，指导产品设计。

绕组是变压器中产生磁场的根源，绕组的形状及其在变压器整体结构中所处的位置，直接影响变压器的漏磁分布。大容量变压器高压绕组一般采用内屏蔽连续式，低压绕组采用螺旋式。连续式绕组由很多个正、反线饼沿轴向串联组成。绕制时，总是若干匝沿辐向串联绕制成一个线饼，然后采用“翻转法”将线饼起头翻到线饼最上面，而将线饼的末头换到最下面的位置，经换位后接着绕第二饼。在连续式绕组中，每一饼线饼都有多匝线匝。饼与饼之间用垫块隔开。而螺旋式绕组是由多根扁导线并联叠绕而成的，饼间都用垫块隔开。根据绕组中电流的大小，绕组可采用单螺旋、双螺旋、3螺旋及4螺旋等结构。螺旋式绕组中每匝有几个线饼就是几螺旋，每匝绕组中饼数越多，绕组的螺旋角越大。因此?n螺旋式绕组的螺旋角大于(n-1)?螺旋的螺旋角。

在查看有关变压器漏磁计算的文献时，发现其中许多文献没有考虑大型变压器螺旋绕组的升角问题，而把所有的绕组都看成是同轴圆环回路，并假设绕组线匝间具有无限薄的绝缘，所有线匝紧密地填充了绕组所占的全部空间，绕组线匝在径向、轴向均匀缠绕，电流沿截面均匀分布。而实际上变压器绕组都是用扁导线一匝挨一匝绕制而成的，每匝之间均具有螺旋性，每个线饼与水平线间夹一固定数值的角度。所以不仅有圆周方向的电流，还有轴向分量的电流，即

特别是多螺旋式绕组的螺旋性更明显，超大容量变压器低压绕组一般采用3螺旋和4螺旋的绕制方式，有的变压器调压绕组还采用8螺旋。因此要计算螺旋式绕组轴向电流分量的影响，必须按照变压器绕组的实际形状建立几何模型。

本文主要针对大型变压器螺旋式绕组的不同螺旋度问题，对变压器漏磁场进行了计算，并根据计算结果，比较了不同螺旋度绕组电流轴向分量对变压器漏磁场的影响程度。

2 物理模型选择

由于螺旋式绕组本身是三维问题、是立体场，同时上下、前后、左右均不对称，无法按对称处理，因此在建立模型时，必须考虑变压器全域。大容量变压器低压螺旋式绕组一般都有100个左右的线饼，饼间都有散热油道间隔，线饼和油道是两种不同的材料，必须进行分别剖分。如果按实际情况建立模型，剖分的信息量相当大，再加上外围高压绕组、铁心、拉板、夹件等构件，按现有的计算资源，无法进行剖分，更不用说漏磁场的计算了。因此，对变压器实际结构必须进行一定的简化处理。

对于多螺旋绕组，按每匝绕组为一个整体向上绕成螺旋体，这样其螺旋角与实际情况完全一致。本文以一台容量为240MVA的单相变压器为计算实例，该台变压器低压绕组采用的是4螺旋式结构，高压绕组采用的是内屏蔽连续式结构。因此建立模型时，为了节省计算资源，高压绕组按同轴圆环处理，低压绕组按不同的螺旋度和无螺旋的情况建立模型。由于受到现有计算资源的限制，本文只计算了低压绕组为32螺旋、16螺旋、8螺旋及无螺旋的四种情况下变压器漏磁场的分布，并分析了各种螺旋度绕组电流轴向分量对漏磁场的影响。对于低压绕组为4螺旋时的变压器漏磁场的计算，在目前计算资源下还无法实现。不过，可根据上述四种情况的计算结果，定性地分析低压绕组为4螺旋时其轴向电流分量对漏磁场的影响。

由于三维涡流场的计算需要更多的计算资源，根据该问题的特点，即主要是研究螺旋式绕组轴向电流分量对变压器漏磁场的影响，因此计算时做了如下假设：

(1)忽略铁心内涡流对漏磁场的影响，认为σ=0。

(2)各金属结构件，包括拉板、夹件、油箱的材料为线性、均匀、各向异性。

(3)忽略位移电流。

(4)忽略高低压绕组内环流、涡流对漏磁场的影响。

(5)计算短路时变压器漏磁分布，即认为一、二次绕组安匝之和为零。

3 求解特点

3.1 利用涡流场求解器求解大型变压器螺旋式绕组问题

本文应用Ansoft低频电磁场计算软件的涡流场求解器求解大型变压器螺旋式绕组问题。涡流场求解器的计算原理是应用电磁场基本方程即Maxwell基本方程。

在工频情况下，忽略位移电流的影响，Maxwell基本方程如下：

3.2 对变压器的油箱采用表面阻抗法

当交变电磁场进入大型导体而透入深度相对很小时，场的梯度将产生急剧的变化。在这种情况下，可足够近似地认为场量在导体内只随沿表面法线方向的梯度变化，使导线内解成为一维的，外部的场看作一等效表面阻抗。这样就使导体区场的描述只限于表面单元，而避

免了内部节点。其表面阻抗可定义为：

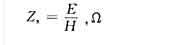
采用表面阻抗法，必须满足下列条件：

(1)导体的集肤深度远远小于它的结构尺寸。

(2)在导体内部，磁场沿表面法线方向衰减比沿切线方向衰减快得多。

(3)交流电源远离涡流场产生的表面。

在变压器中，一般油箱选用A3钢，根据集肤深度计算公式：

式中ω源电流的角频率，rad/s

σ材料的电导率，S/m

μr材料的相对磁导率

μ0真空中的磁导率，H/m

对于A3钢，σ=5.6×106S/m，μr=200，代入式(5)可得油箱的集肤深度δ=1.5mm，远小于油箱的结构尺寸，因此可将油箱内表面作为阻抗边界。在建立模型时，油箱本身并不包括在求解区域内，而将油箱的内表面作为求解边界。这样可避免在油箱内作剖分及求解，可节约计算资源。

4 不同螺旋度螺旋式绕组的变压器漏磁场分布计算结果分析

4.1 螺旋式绕组轴向电流分量对铁心最小级表面漏磁场的影响

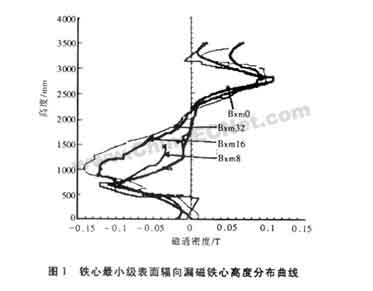
各种螺旋度螺旋式绕组轴向电流分量对铁心最小级表面漏磁场的影响见图1。由图1可以看出，不同螺旋度螺旋式绕组轴向电流分量在铁心最小级表面辐向本文提到的辐向、轴向、周向均指变压器低压侧正对绕组中心位置。漏磁分布总的趋势是相同的，即在绕组两端辐向漏磁较大，而在绕组中部漏磁较小。不同之处是各不同螺旋度螺旋式绕组漏磁峰值范围不同。螺旋度越大的绕组，在绕组两端的峰值范围较大，即在最大值附近变化较缓，而无螺旋的绕组在绕组两端的峰值较尖，在离开绕组两端位置磁密下降较快。而在绕组中部，磁密过零改变方向时，螺旋度越大的绕组，磁密变化也越快，无螺旋时磁密变化较缓。从图形来看，与无螺旋相比，32螺旋绕组轴向分量对铁心最小级表面漏磁场的影响较大，16螺旋绕组次之，8螺旋绕组影响较小。从4条曲线的分布关系看，可定性地判断出当低压绕组为4螺旋时，其铁心最小级表面辐向漏磁分布曲线应在Bxm0与Bxm8之间。因此，可以认为当低压绕组为4螺旋时，其轴向电流分量对铁心最小级表面漏磁场的影响很小，可以忽略不计。

4.2 螺旋式绕组轴向电流分量对拉板外表面漏磁场的影响

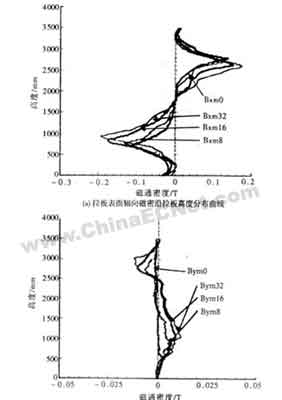
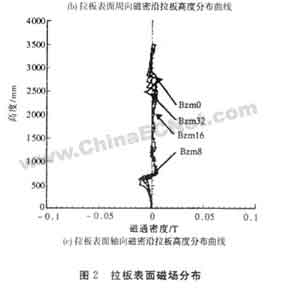
各种螺旋度螺旋式绕组轴向电流分量对拉板外表面漏磁场的影响如图2所示。其中图2a为不同螺旋度低压绕组变压器拉板外表面辐向磁密沿拉板高度的分布曲线。由图2可以看出，不同螺旋度螺旋绕组在拉板外表面辐向漏磁分布总的趋势相同，即在绕组两端磁密最大，在绕组中部漏磁通过零且改变漏磁方向。但4条曲线的具体分布是不同的，其分布规律为随着螺旋式绕组螺旋角的增大，漏磁最大值出现的位置向绕组中部偏移，最大值也相应增大。在漏磁点通过零点附近，螺旋角较大的绕组，其磁密变化的梯度较大；而无螺旋时，磁密变化的梯度最小。因此，通过对图2a的4条曲线的比较，可以看出32螺旋式绕组轴向分量对拉板外表面漏磁场的影响最大，16螺旋次之，8螺旋与无螺旋两条曲线比较接近。因此可定性地判断出当低压绕组为4螺旋时，其拉板表面辐向漏磁分布曲线应在Bxm0与Bxm8之间，因此可以认为当低压绕组为4螺旋时，其轴向电流分量对拉板外表面漏磁场的影响很小，可以忽略不计。图2b为拉板外表面周向磁密沿拉板高度的分布曲线，由图可以看出，在无螺旋时，拉板表面周向磁密很小，基本为零。随着低压绕组螺旋角的增大，在绕组两端的周向磁密越来越大，但与辐向磁密相比，低一个数量级。图2c为拉板外表面轴向磁密沿拉板高度的分布曲线。

4.3 各种螺旋度螺旋式绕组轴向分量对低压绕组外表面漏磁场的影响

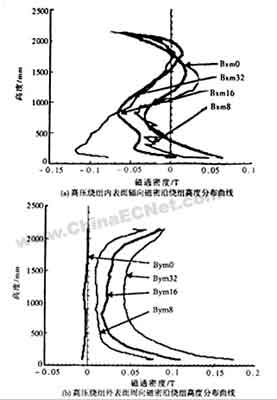
各种螺旋度螺旋式绕组轴向分量对低压绕组外表面漏磁场的影响见图3。其中图3a为不同螺旋度低压绕组外表面辐向磁密沿绕组高度的分布曲线，由图可以看出不同螺旋度螺旋式绕组在低压外表面辐向漏磁分布在绕组两端磁密较大，在绕组中部漏磁通过零且改变漏磁方向。其分布规律为随着螺旋式绕组螺旋角的增大，漏磁最大值相应增大。在漏磁通过零点附近，螺旋角较大的绕组，其磁密变化的梯度较大；而无螺旋时，磁密变化的梯度最小。因此，通过对图2a的4条曲线的比较，可以看出32螺旋式绕组轴向分量对低压绕组外表面漏磁场的影响最大，16螺旋次之，8螺旋与无螺旋两条曲线比较接近，影响最小。因此可定性地判断出当低压绕组为4螺旋时，低压绕组外表面辐向漏磁分布曲线应在Bxm0与Bxm8之间，进而可以认为当低压绕组为4螺旋时，其轴向电流分量对低压绕组外表面漏磁场的影响很小，可以忽略不计。图3b为低压绕组外表面周向磁密沿绕组高度的分布曲线。由图可以看出，在无螺旋时，低压绕组内表面周向磁密很小，基本为零；随着低压绕组螺旋角的增大，在绕组两端的周向磁密越来越大，在绕组中部磁密也有所增加，特别是32螺旋式绕组，其周向磁密在绕组两端及中部均较大。图3c为低压绕组外表面轴向磁密沿绕组高度的分布曲线，4条曲线总的分布趋势是相同的，即在绕组中部磁密最大，在绕组两端磁密下降。

4.4 各种螺旋度的螺旋式绕组轴向分量对高压绕组内表面漏磁场的影响

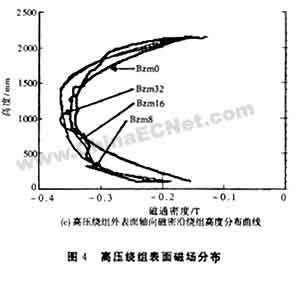
各种螺旋度螺旋式绕组轴向分量对高压绕组内表面漏磁场的影响见图4。其中图4a为不同螺旋度低压绕组变压器，其高压绕组内表面辐向磁密沿绕组高度的分布曲线。图4b为高压绕组内表面周向磁密沿绕组高度的分布曲线，由图可以看出，在无螺旋时，高压绕组内表面周向磁密 小，基本为零；随着低压绕组螺旋角的增大，在绕组两端的周向磁密越来越大，在绕组中部磁密也有所增加，其分布规律与低压绕组外表面周向磁密的分布很相似。这说明螺旋绕组轴向分量对周向磁密有一定的影响。特别是在绕组的两端影响要大一些。图4c为高压绕组内表面轴向磁密沿绕组高度的分布曲线，4条曲线磁密在绕组中部磁密较大，在绕组两端较小。

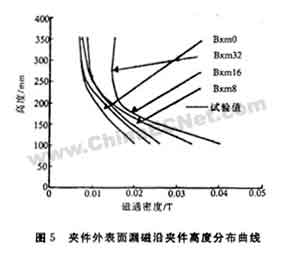
4.5 不同螺旋度的螺旋式绕组在夹件表面的漏磁分布及与试验结果的比较

图5为四种螺旋度螺旋式绕组变压器在夹件表面的辐向漏磁分布及在该处的实测值的分布曲线。由图5可以看出，在四种情况下，趋势是一致的，即在夹件下端辐向漏磁较大，到夹件上端漏磁逐渐减小。在下端，32螺旋漏磁最大，0螺旋最小，在上端，除32螺旋外，其它的漏磁较小，且比较接近，这表明螺旋绕组的轴向电流分量对夹件下端影响较大，对夹件上端基本没有影响。且随螺旋角的增大，影响也增大。实测值曲线在无螺旋与8螺旋之间，这是由于实际产品是4螺旋式绕组，这也证明了本论文的计算模型是可信的。

5 结论?

本文根据四种螺旋式结构即32螺旋、16螺旋、8螺旋和无螺旋的情况下变压器漏磁场的计

算结果分析，可得出如下结论：?

(1)不同螺旋度绕组变压器在铁心及拉板表面辐向漏磁分布总的趋势是一致的，即在绕

组两端辐向漏磁较大，而在绕组中部漏磁较小。不同之处是各不同螺旋度螺旋式绕组漏磁峰值范围不同，螺旋度越大的绕组，在绕组两端的峰值范围较大，即在最大值附近变化较缓，而无螺旋的绕组在绕组两端的峰值较尖，在离开绕组两端位置磁密下降较快。而在绕组中部，磁密过零改变方向时，螺旋度越大的绕组，磁密变化也越快，无螺旋时磁密变化较缓。

(2)随着螺旋式绕组螺旋角的增大，在低压绕组的内、外表面辐向漏磁最大值相应增大。

在漏磁过零点附近，螺旋角较大的绕组，其磁密变化的梯度较大；而无螺旋时，磁密变化

的梯度最小；在低压绕组的外表面及高压绕组内表面周向漏磁也随螺旋角的增大而增加。但随着螺旋式绕组螺旋角的增大，在各处的轴向漏磁分量有略微改变，这主要是由于随着螺旋式绕组螺旋角的增大，绕组的周向电流分量减小引起的。

(3)实际变压器采取的4螺旋式结构，对漏磁的影响应在0螺旋和8螺旋之间，由所有的漏磁分布曲线来看，从工程的角度出发，认为其影响不会很大。

来源：《变压器》